
平行线的判定:1、同位角相等,两直线平行;2、内错角相等,两直线平行;3、同旁内角互补,两直线平行;4、两条直线平行于第三条直线时,两条直线平行;5、在同一平面内,垂直于同一直线的两条直线互相平行;6、在同一平面内,平行于同一直线的两条直线互相平行;7、同一平面内永不相交的两直线互相平行。
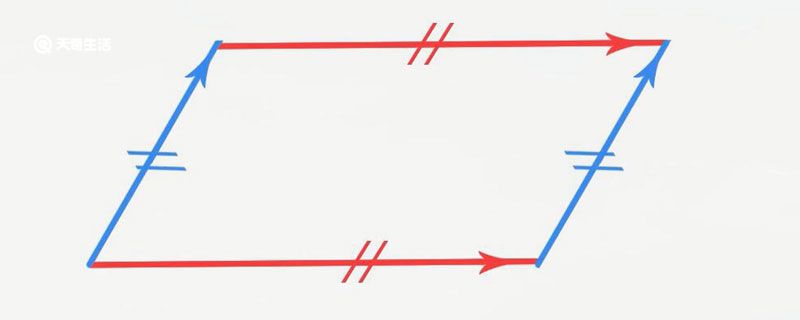
在几何中,在同一平面内,永不相交也永不重合的两条直线叫做平行线。平行线的定义包括三个基本特征:一是在同一平面内,二是两条直线,三是不相交。平行线一定要在同一平面内定义,不适用于立体几何,比如异面直线,不相交,也不平行。
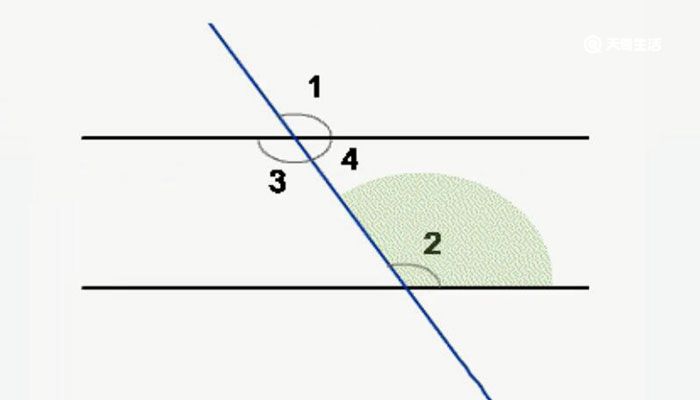
在高等数学中的平行线的定义是相交于无限远的两条直线为平行线,因为理论上是没有绝对的平行的。在同一平面内,两条直线的位置关系只有两种:平行和相交。
平行线的判定是由角的数量关系来确定线的位置关系,而平行线的性质则是由线的位置关系来确定角的数量关系,平行线的性质与判定是因果倒置的两种命题。对平行线的判定而言,两直线平行是结论,而对平行线的性质而言,两直线平行却是条件。
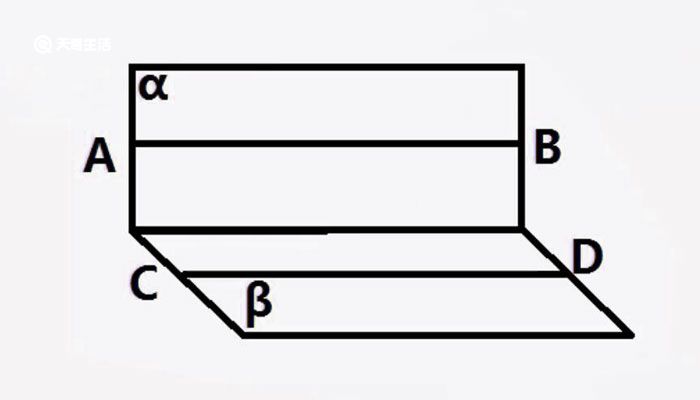
已知两直线平行,由平行线得到角的关系是平行线的性质,包括:1、两直线平行,同位角相等;2、两直线平行,内错角相等;3、两直线平行,同旁内角互补。





